2.4 Value Iteration and Policy Iteration (策略迭代与truncated iteration)

前置知识

2.3 Value Iteration and Policy Iteration (值迭代)

策略代算法流程

• 第一步：给定一个随机初始策略，计算状态值

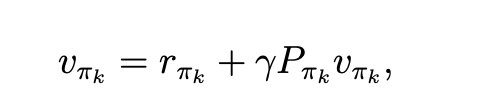
  这里计算状态值， 使用了1.2 State Values and Bellman Equation (Vector form 与 求解)所述的迭代过程。

• 第二步：更新策略

  求得了状态值后，使利用它找到每个状态的最大的action value，从而更新策略

  

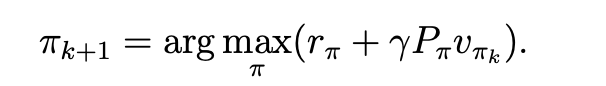
• 迭代：更新完策略后，再用新策略计算状态值，等于大迭代里套小迭代。

具体实现

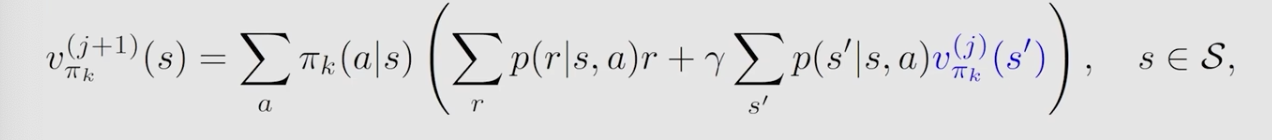
\(v_{\pi_k}^{(j)}\left(s^{\prime}\right)\) 为第k次迭代算到的状态值，策略是给定的，其他都是已知的，因此可以算得第k+1次的状态值。算到了状态后，再用来更新策略，如下：

\(\pi_{k+1}(s)=\arg \max _\pi \sum_a \pi(a \mid s) \underbrace{\left(\sum_r p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_{\pi_k}\left(s^{\prime}\right)\right)}_{q_{\pi_k}(s, a)}, \quad s \in \mathcal{S}\),

找到了策略后，再用来计算下一次的状态值，如此迭代。

Truncated policy iteration

策略迭代中，从初始策略开始

• Policy Evaluation (PE)，计算状态担

  \(v_{\pi_k}=r_{\pi_k}+\gamma P_{\pi_k} v_{\pi_k}\).

• Policy Improvement (PI), 更新策略

  \(\pi_{k+1}=\arg \max _\pi\left(r_\pi+\gamma P_\pi v_{\pi_k}\right)\).

值迭代，从值出发

• Policy update (PU): 利用给定的假状态值，直接更新策略

  \(\pi_{k+1}=\arg \max _\pi\left(r_\pi+\gamma P_\pi v_k\right)\).

• Value Update (VU): 更新完策略后，利用新策略和旧的假状态值得到新的状态值

  \(v_{k+1}=r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}} v_k\)

比较

Policy iteration: \(\pi_0 \xrightarrow{P E} v_{\pi_0} \xrightarrow{P I} \pi_1 \xrightarrow{P E} v_{\pi_1} \xrightarrow{P I} \pi_2 \xrightarrow{P E} v_{\pi_2} \xrightarrow{P I} \ldots\) Value iteration: \(\quad v_0 \xrightarrow{P U} \pi_1^{\prime} \xrightarrow{V U} v_1 \xrightarrow{P U} \pi_2^{\prime} \xrightarrow{V U} v_2 \xrightarrow{P U} \ldots\)

其实是非常类似的。 我的看法是，2个算法的区别在于是否真的要算状态值，值迭代方法每次在算状态值的时候就算一次，然后就来更新策略，策略迭代算法每次都要把状态值完美地算出来，再来更新策略

这2个方法是2个极端，因此在truncated iteration中，每次指定一个阈值，用来限制计算状态值时的迭代次数，虽然也是迭代套迭代，但不致于要算出每个策略最终的状态值，因为没有必要。

truncated policy iteration

用一个图表示这个算法，其实就是前2个算法的折中方法。

总结

• BOE，定义，表达
• BOE的求解
• 值迭代与策略迭代
• truncated policy iteration