2.1 Optimal State Values and Bellman Optimality Equality
前置知识
State Values and Bellman Equation (Basic and Definition) 1
State Values and Bellman Equation (Vector form 与 求解) 2
State Values and Bellman Equation (Action value and Summary) 3
请学会前置知识再看本节
本部分重点
- 最优状态值(optimal state value) 最优策略 (optimal policy)
- Bellman optimality equation (BOE) (用于寻找上面最优策略的工具)
策略更新的例子
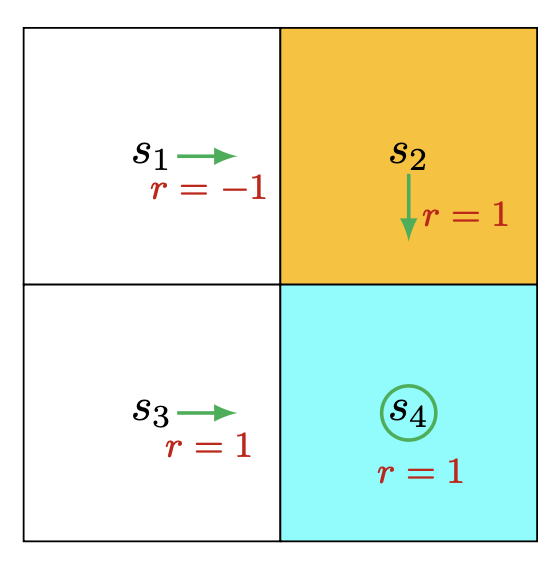
对于这个例子,我们先求每个状态的state value, 结果如下(当前状态的reward + discount * 未来状态的state value):
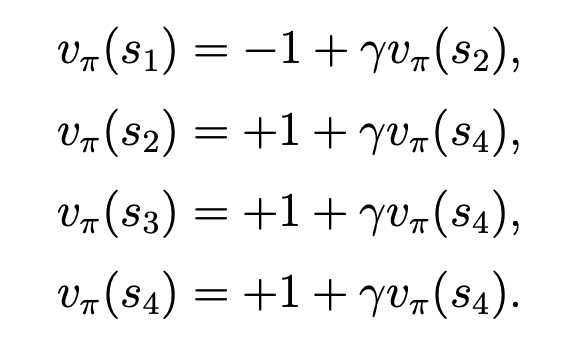
当我们取discount = 0.9时,可求得每个状态的state value 为:
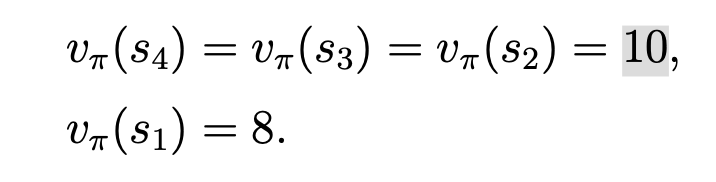
再根据这些state value, 求得在s1时它的所有的 action value:
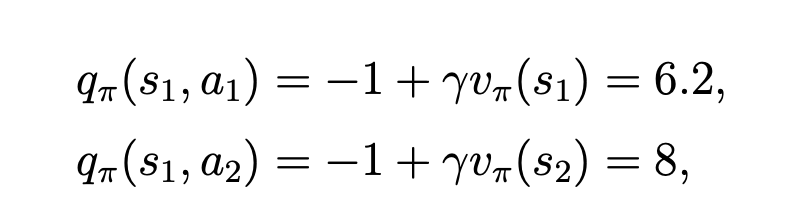
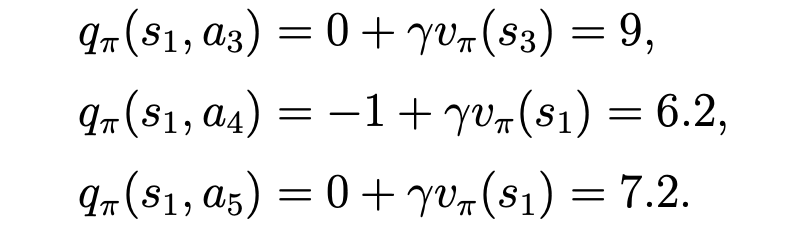
从结果可以看到,s1处的 a3的action value 是最大的。
而当下的策略如下:
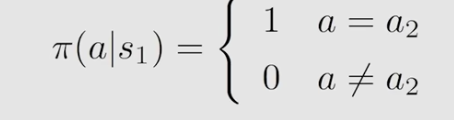
即在s1处,采用当下的策略,一定会选择的action = a2。
但其实在s1状态时,a3的action value是最大的,所以我们可以对当下的策略做一个更新,即新策略为:
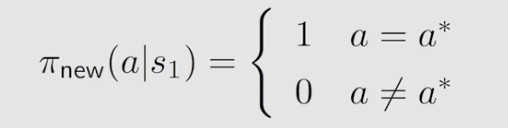
即更新的时候,在每个状态选择action value最大的那个:
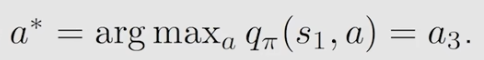
策略评估
当说一个策略比另一个策略好,要求是在这个策略上,其所有状态的state value 都优于另一个策略的state value,表达如下:
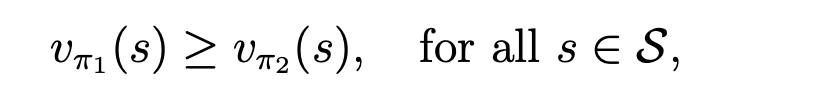
因此最优策略即为:其state value要比所有的其他策略都好
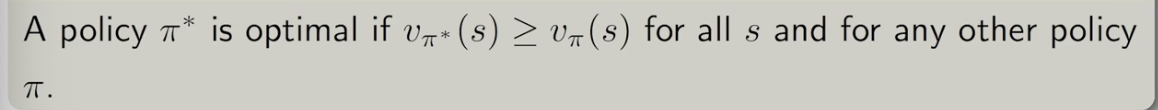
需要注意的是:
- 最优策略是否存在
- 最优策略是否唯一
- 最优策略是随机性的还是确定性的
- 如何找到最优策略
Bellman Optimal Equation 定义
其实定义比较抽象,即是在原来的bellman equation的前面加了个max, 如下:
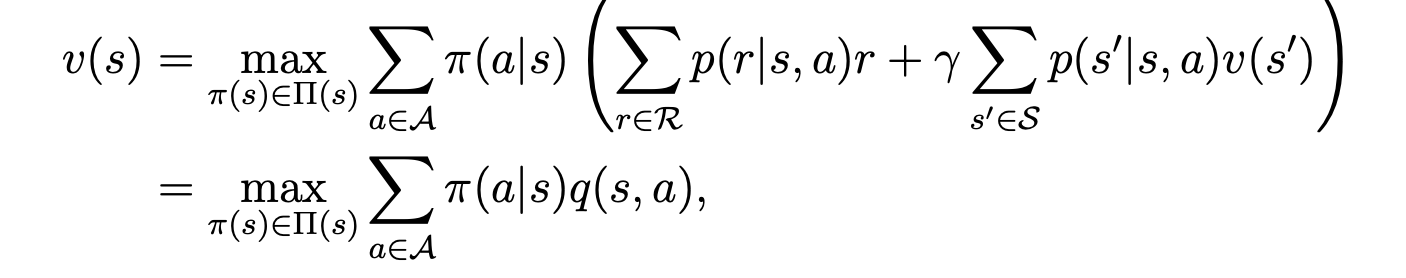
它的矩阵向量形式如下:
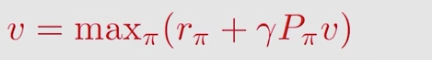
其中:
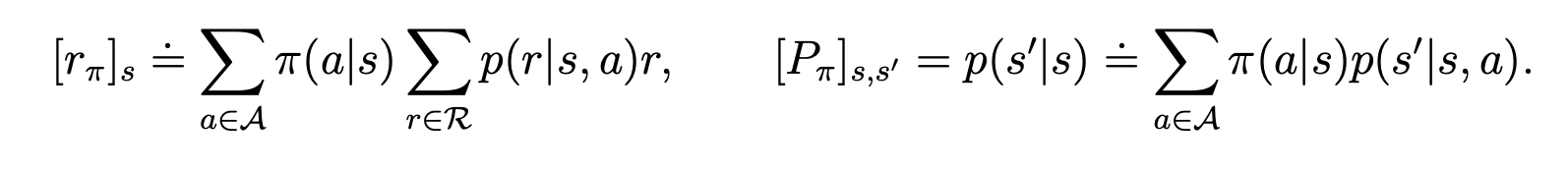
公式的第二行是使用了action value的表达。
在bellman equation里面,有多少个state, 就有多少个equation,使我们可以刚好求得所有的state value。
但是在这里,多了一个未知量,即\(\pi\), 是我们要求的策略。
这里主要有一个数学技巧,
-
可能性:等式不够,在某些特定情况下也可以求得变量值,例子如下:
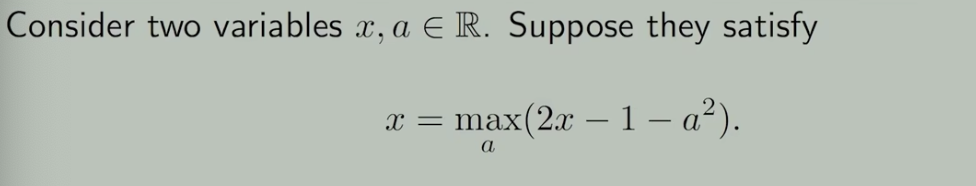
这里要求满足条件的x的值,很容易。
-
求解方法
看bellman optiml equation 的action value形式,然后对照着看下面的例子:
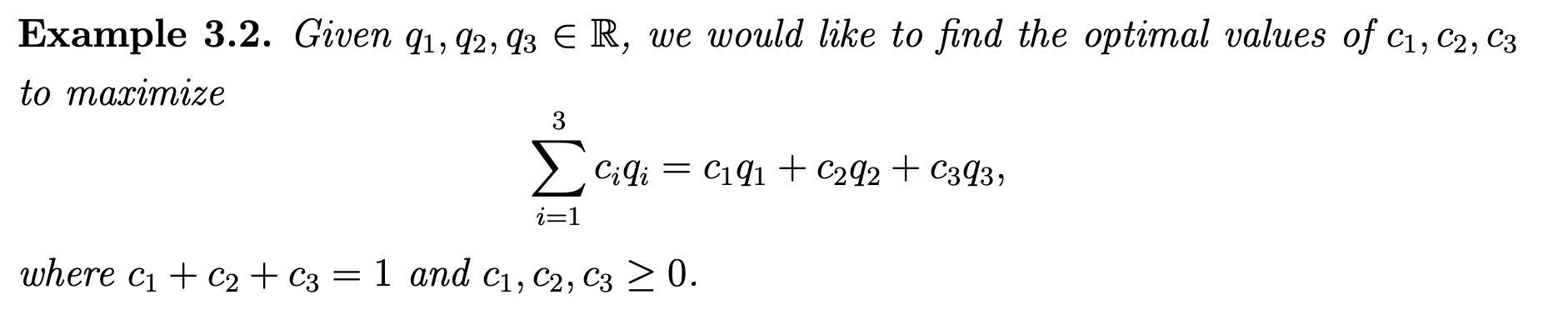
这个例子里的c其实就是公式里的\(\pi\), 而q就是公式里的action value.
要求例子的结果,首先要对比所有的q,然后找到最大的,将最大的q前面的系数选择最大,其他q的系数都选0即可,原因如下:
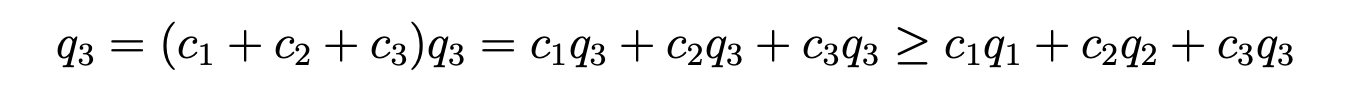
所以在解bellman optimize equation时,在算得了所有的action value后,更改现有策略将将所有状态的action都选对应action value最大的那个,如此迭代最后即可找到最优策略,表达如下:
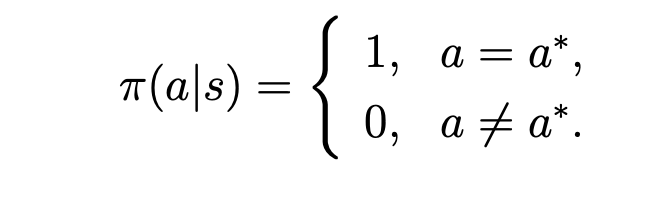
文若可采,幸赐清茗一盏,以助笔耕不辍
