2.3 Value Iteration and Policy Iteration (值迭代)

前置知识

2.2 Optimal State Values and Bellman Optimality Equality (BoE 求解)

Value Iteration Algorithm

回忆一下BOE的形式

\(v_{k+1}=\max _{\pi \in \Pi}\left(r_\pi+\gamma P_\pi v_k\right), \quad k=0,1,2, \ldots\)

在使用它求解BOE的时候，其产是分2步进行的

• 第一步：策略更新

  针对给定的\(v_k\)，求得更新后的策略\(\pi_{k+1}\)

  \(\pi_{k+1}=\arg \max _\pi\left(r_\pi+\gamma P_\pi v_k\right)\)

• 第二步：值更新

  针对求得的新的策略，计算value 值\(v_{k+1}\)

  \(v_{k+1}=r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}} v_k\)

这里要注意的是，上述迭代过程中,\(v_k\) 并不是state value.

也就是说，初始时候给定的一个\(v_k\),我们直接拿它算所有动作值，再利用动作值更新策略，更用策略和BOE计算新的\(v_k\)，此过程中的每一步的\(v_k\)都不是state value，它只是根据新的策略算出来的一个向量，前面说过其实可以利用迭代法计算出真正的\(v_k\)，但是此过程中并没有这么算。如果每一次都算出真正的\(v_k\)，那么恭喜你，学会了Policy Iteration算法。

如何求新策略：

1. 首先求得所有的q

   \(\pi_{k+1}(s)=\arg \max _\pi \sum_a \pi(a \mid s) \underbrace{\left(\sum_r p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_k\left(s^{\prime}\right)\right)}_{q_k(s, a)}, \quad s \in \mathcal{S}\)

2. 更新action， 策略动作价值最大的action来替换原策略中的action：

   \(\pi_{k+1}(a \mid s)= \begin{cases}1, & a=a_k^*(s) \\ 0, & a \neq a_k^*(s)\end{cases}\)

如何进行值更新：

\(v_{k+1}(s)=\sum_a \pi_{k+1}(a \mid s) \underbrace{\left(\sum_r p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_k\left(s^{\prime}\right)\right)}_{q_k(s, a)}, \quad s \in \mathcal{S}\).

利用新的策略代入旧式子，即可获得新的value。

例子

对于一个问题，参数设置：

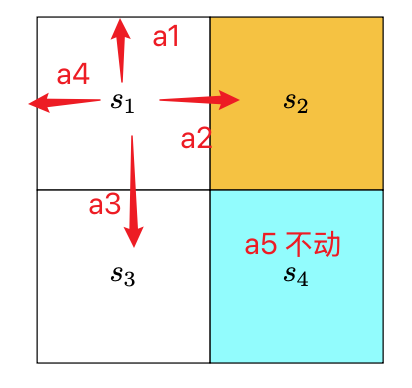
初始状态图片：

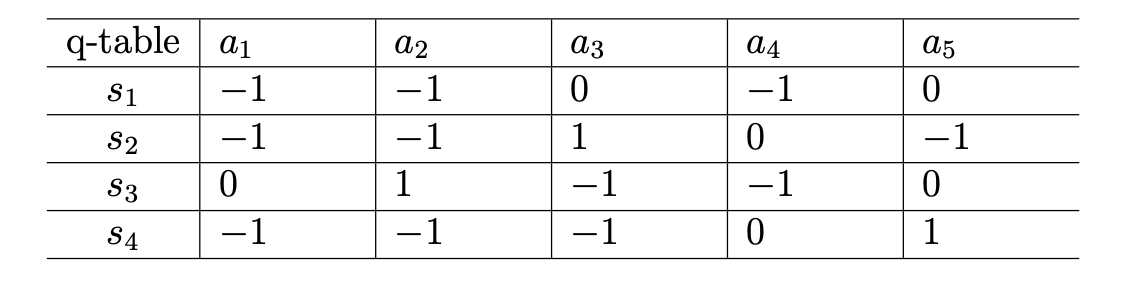
列出所有的状态对应的action的action value，获得一个q表，如下：

现在给所有的v（s）一个初始值0，代入这个q表中获昨新表：

这时更新每一个状态s处的策略，选择最大的那个，即如果在s1处，策略选a3或a5，这里选的是a5,其他状态类似，得到

策略为：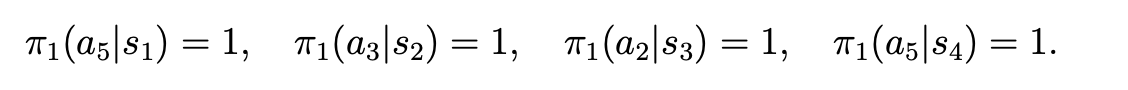

更新每个状态的value （这里是利用了亲的的策略和旧的value \(v_0\)计算得新的\(v_1\)）:

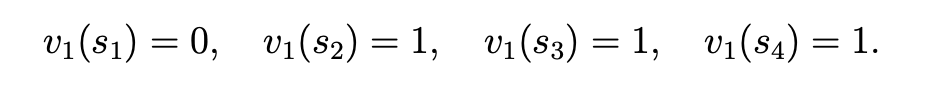
新的策略，其图如下：

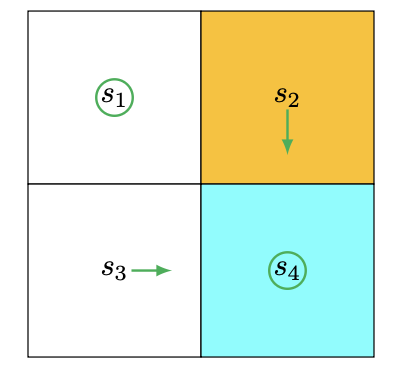
利用新的v值，代入q表中，获得：

此时再用新表结果，更新策略，得到的策略图：

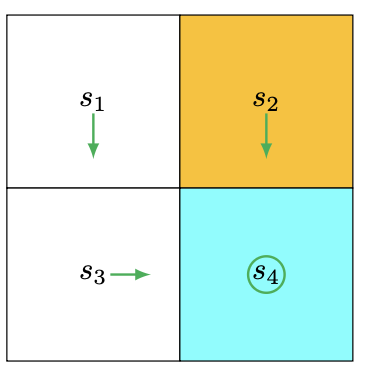
这过程可以看到，并没有在每一步都要求出它的状态值，也就是说不管这个状态值真不真，一直迭代到最后都能获得最优策略，这就是神奇之处

Policy Iteration Algoritym

Truncated Policy Iteration Algorithm