2.2 Optimal State Values and Bellman Optimality Equality (BoE 求解)

前述知识

2.1 Optimal State Values and Bellman Optimality Equality

BoE 定义

在2.1 Optimal State Values and Bellman Optimality Equality中定义的最优公式为：

\[ v=\max _{\pi \in \Pi}\left(r_\pi+\gamma P_\pi v\right) \]

这里我们将右边定义为 f(v)，即v是一个f(v)函数的变量：

\[ f(v) \doteq \max _{\pi \in \Pi}\left(r_\pi+\gamma P_\pi v\right) . \]

因此，可得的BoE为：\(v = f(v)\)。

而将它写成向量形式可表示为：

\[ [f(v)]_s=\max _\pi \sum_a \pi(a \mid s) q(s, a), \quad s \in \mathcal{S} \]

如何求解呢

Fixed Point

对于一个X到X的映射f(x)， 若有一个\(x \in X\)，满足： \(f(x) = x\)，那么x就是\(f(x)\)的一个不动点

Contraction mapping:

若一个函数 f , 其满足：

\[ \left\|f\left(x_1\right)-f\left(x_2\right)\right\| \leq \gamma\left\|x_1-x_2\right\| \]

其中， \(\gamma < 1\)则 f 为contraction mapping.

下面是fixed point 和 Contraction mapping的例子

这2个概念也可扩展到向量维度

定理

映射f(x), 当 f 是一个contraction mapping时，则：

• 一定存在\(x^{*}, f(x^{* }) = x^{*}\)
• \(x^{*}\) 是唯一存在的
• 这个值可通过迭代法找到，且收敛速度为指数

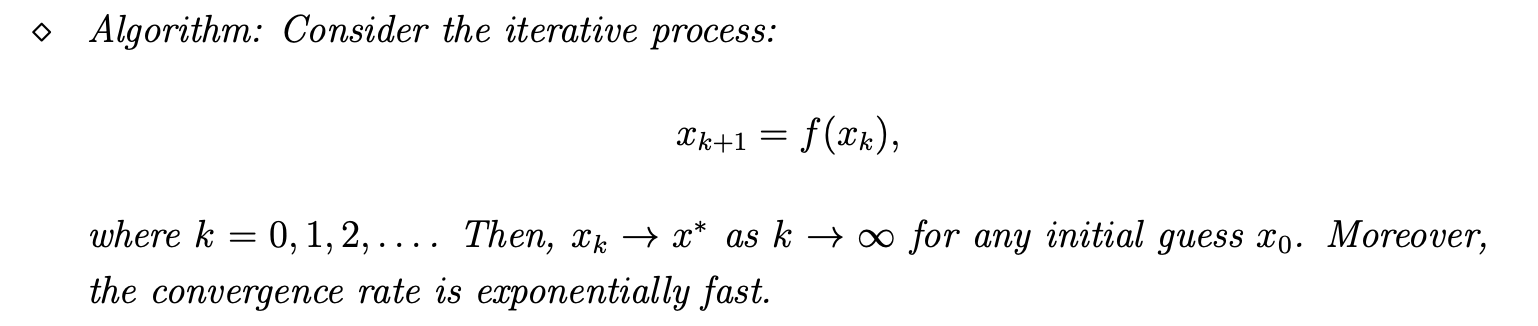
证明过程请付费收看

举个例子

\(f(x) = 0.5 x\). x = 0 显然为不动点。如何求呢，假设\(x_{0} = 10\)，求得\(f(10) = 5\), 得\(x_{1} = 5\), 如此继续，\(x_{2}=2.5\) ，很快就可求得结果。

同样，对于矩阵形式\(f(x) = Ax\), 也可得类似结果。

将定理应用到BoE求解中

前面BoE表达式为：\(v=f(v)=\max _\pi\left(r_\pi+\gamma P_\pi v\right)\) , 可以看到和前面的contraction mapping 是一个类型的。根据求述，其一定有最优解，最优解唯一，且使用迭代方法可求得: \(v_{k+1}=f\left(v_k\right)=\max _\pi\left(r_\pi+\gamma P_\pi v_k\right)\).

大概思考了下求最优策略的过程，因为求v的过程是迭代的，而求策略又得迭代求出来的v，所以是迭代里面套迭代

这里的BoE式子满足contraction mapping可证，证明过程付费观看

当求得最优策略后，其对应的state value \(v^{*}\)一定满足：

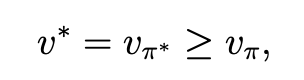
过程可证，付费观看

思考

• 什么因素会决定最优策略？

  

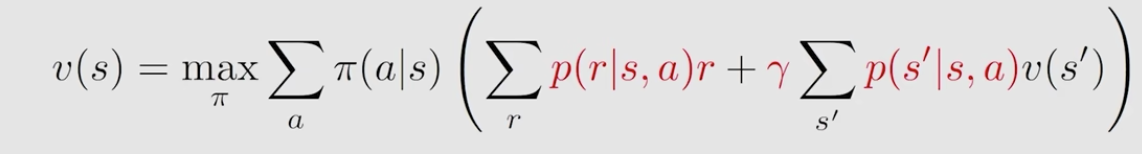
  红色为已知量，求BoE过程即是求黑色变量。 其实我认为2个p会在迭代过程中不断被更新，所以真正的已知量，需要手动设置的是r和\(\gamma\)

在一个例子中，我们设定好了已知量，其最终求得的策略和状态值如下：

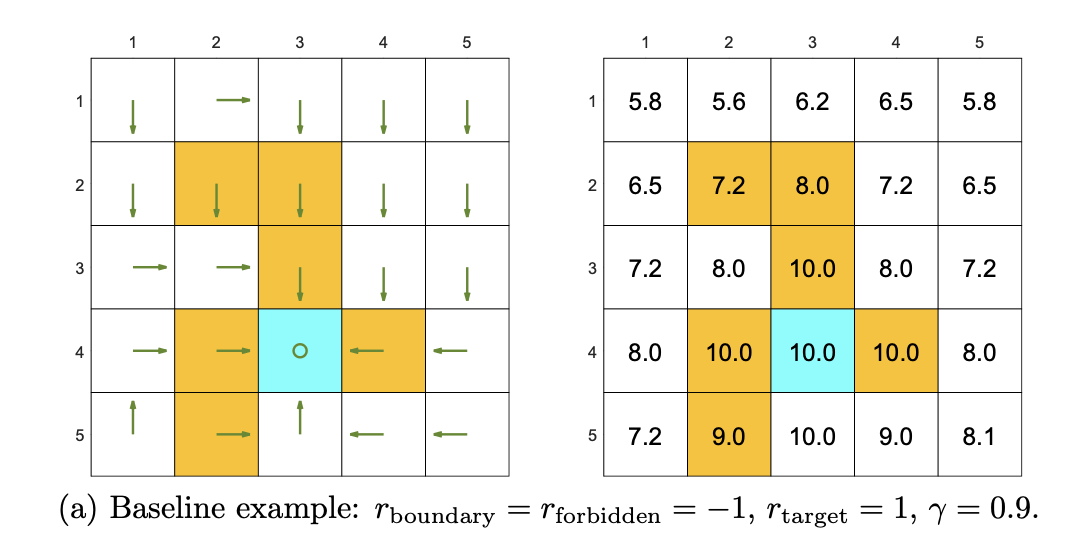
这里可以看到，虽然给黄色区域设置了惩罚，但根本不会管

下面将discount 值\(\gamma\)改小一点，结果变了：

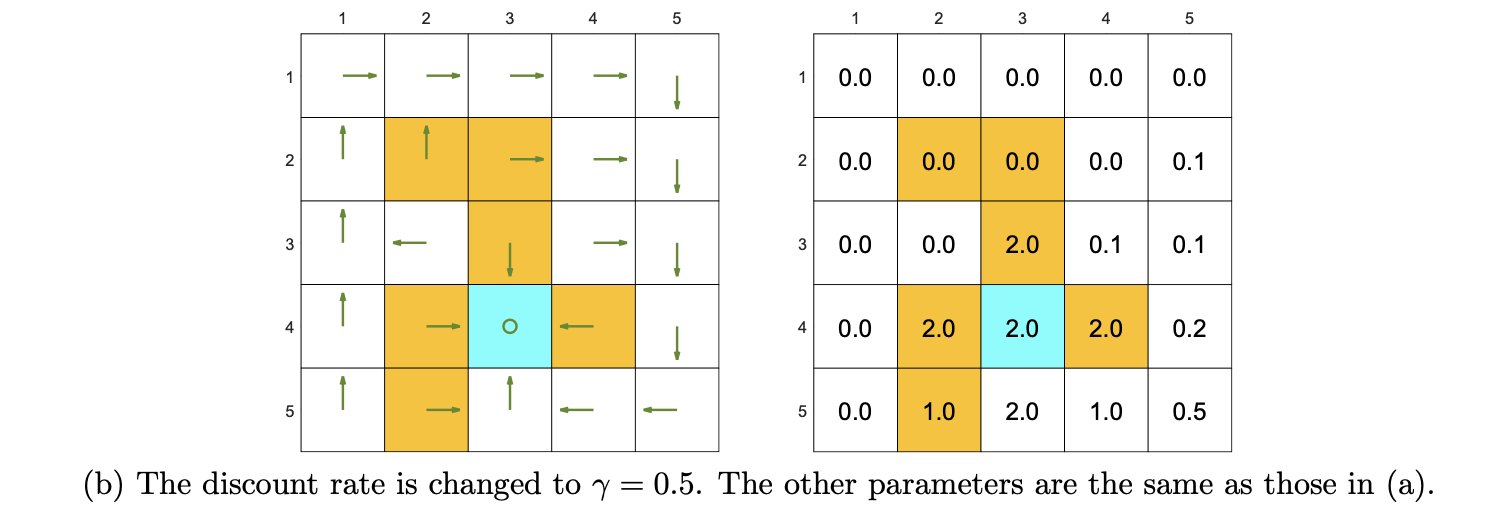
可以看到，宁愿绕最远的路，也不进黄色区域。当\(\gamma\)大的时候，其实更能获得远视的收益，而当它小的时候，最终的收益是由近的action决定的，在b例子中值小，如果进了黄色区域，那一开始的黄色区域惩罚对最终的收益影响更大，所以宁愿绕路也不进黄区。

再看个例子：

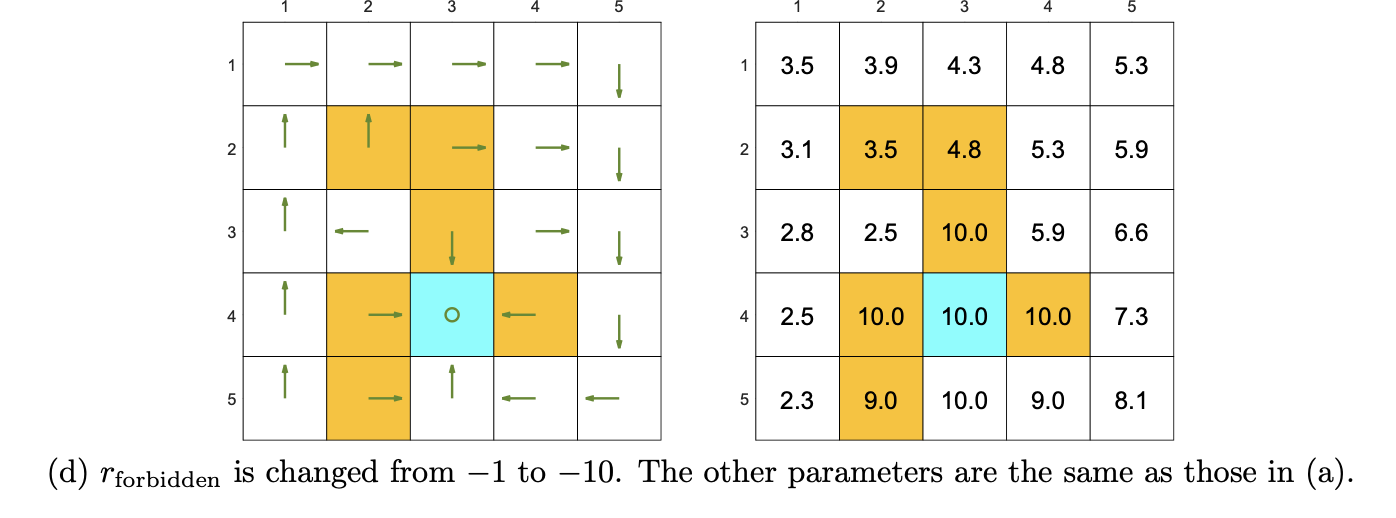
这里加大了惩罚力度，即使\(\gamma\)大，但惩罚太子了，影响了最后的收益，所以也会导致绕嘱

• 最优策略依据的是相对 reward

  例如如下设置的2个不同的reward：

  

  这2个reward最后求得的最优策略其实会是相同的，因为相对reward没变，直观的理解就是更新策略的时候使用的是action value最大的那个动作，而相对reward就决定了哪个action value最大，因此最后获得的策略没变。。

  如果相对reward没变，那策略也不会变，过程可证，证明过程付费观看。

• 自动避免无效绕路

  

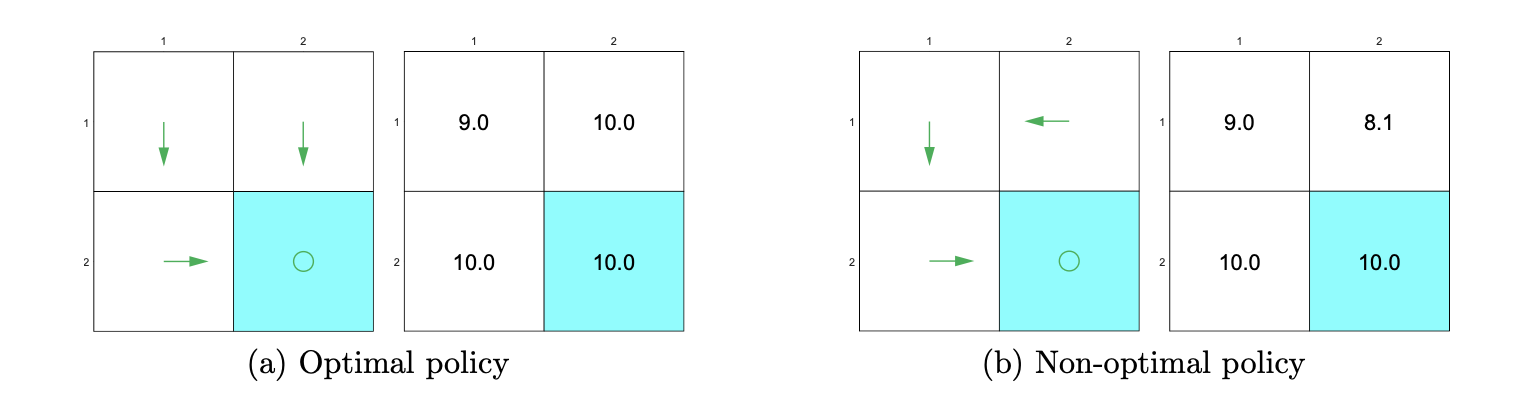
  在设置reward的时候，并未设置惩罚，但最优策略会避免绕路过程，这是因为\(\gamma\)的存在，绕路的过程会使最终的收益变小