1.2 State Values and Bellman Equation (Vector form 与 求解)

矩阵向量形式

本节接State Values and Bellman Equation 1, 请将上节的前置知识看完再看本节

完整公式为：

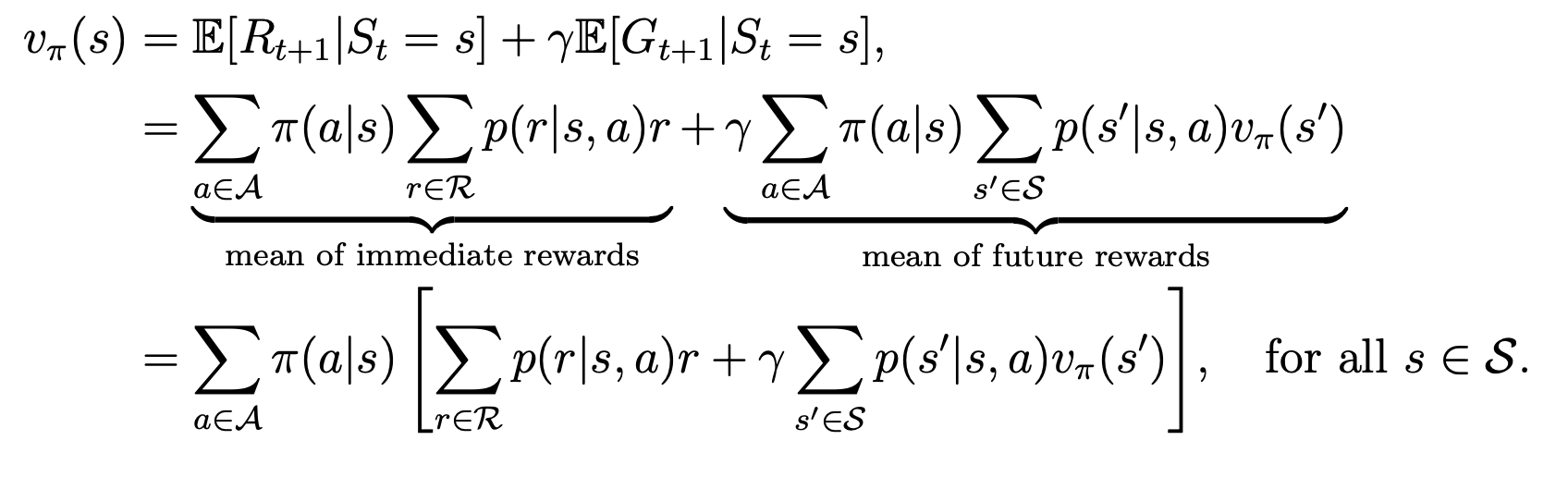这里的未知量有2个，\(v_{\pi}(s)\)和\(v_{\pi}(s’)\). 一个式子是没法求出2个未知量的，但是因为对每一个状态都有一个式子，因此可以通过联立求得每一个状态的状态值。

将这个式子重新表达下如下：

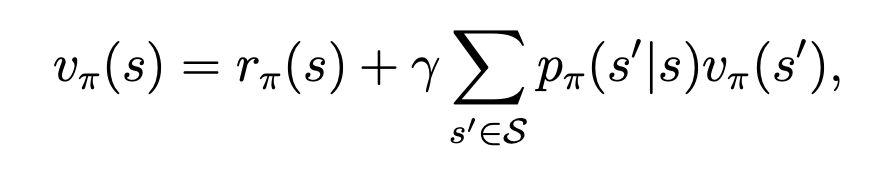
其中，

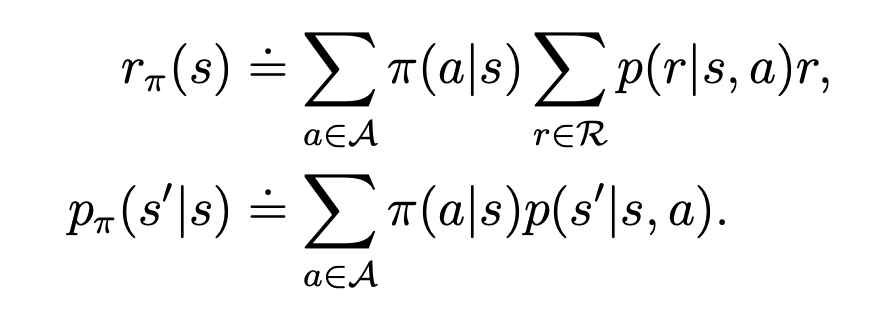
重写的式子更有直观性，可理解为当下状态的状态值为当下reward与下个状态的reward的和。

将每个状态都标上下标，可写作：

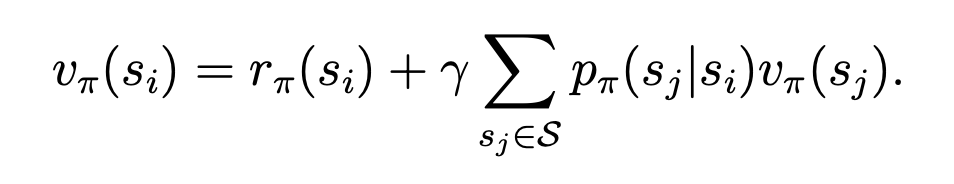
这个式子可进一步写成矩阵向量形式：

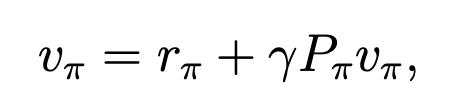
其中，各个字母意义如下：

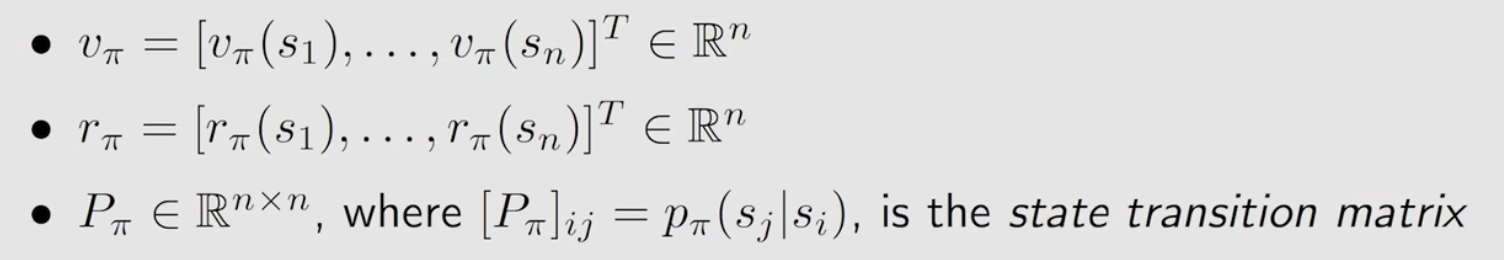
举个例子，如果有4个状态，那它的矩阵向量形式可写为：

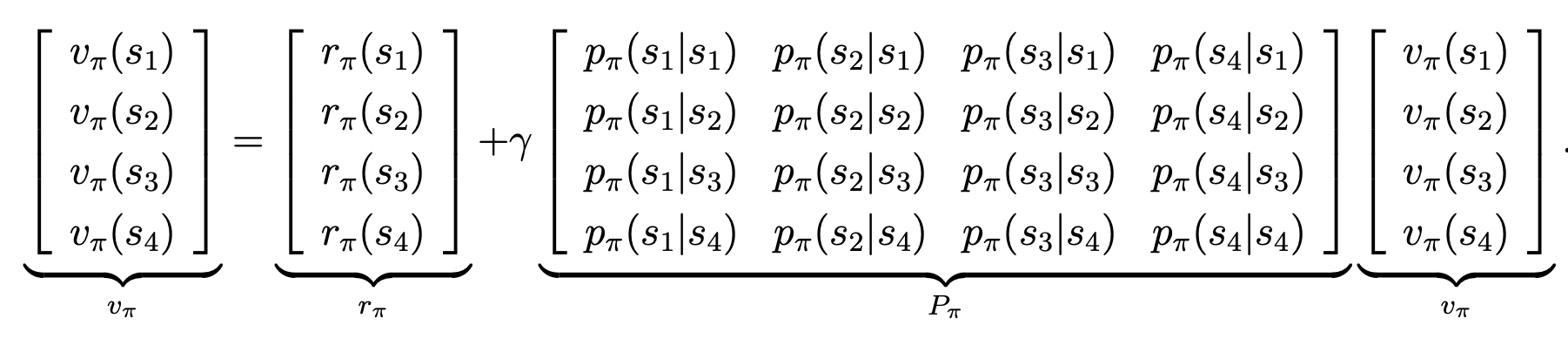
举例说明1

对于下图的例子

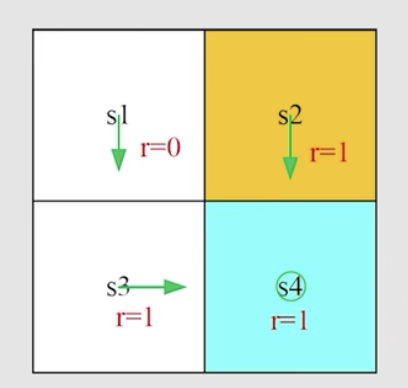
它的矩阵形式可表达为：

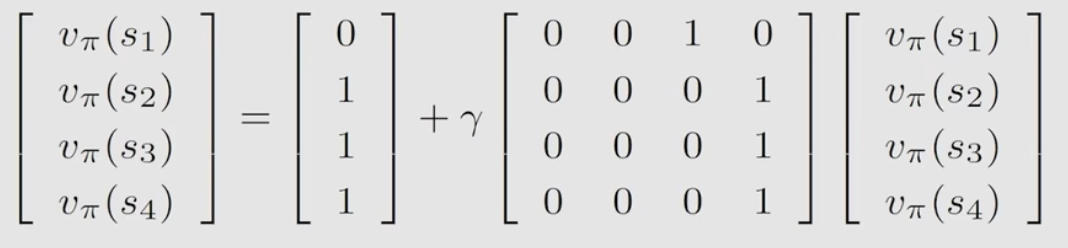
举例说明2

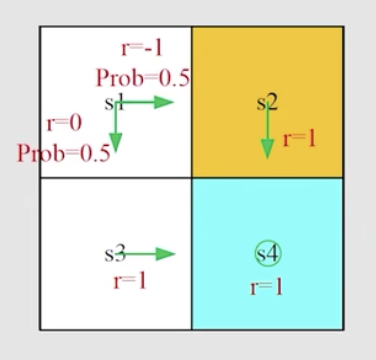
对于上面的例子，它的矩阵形式为：

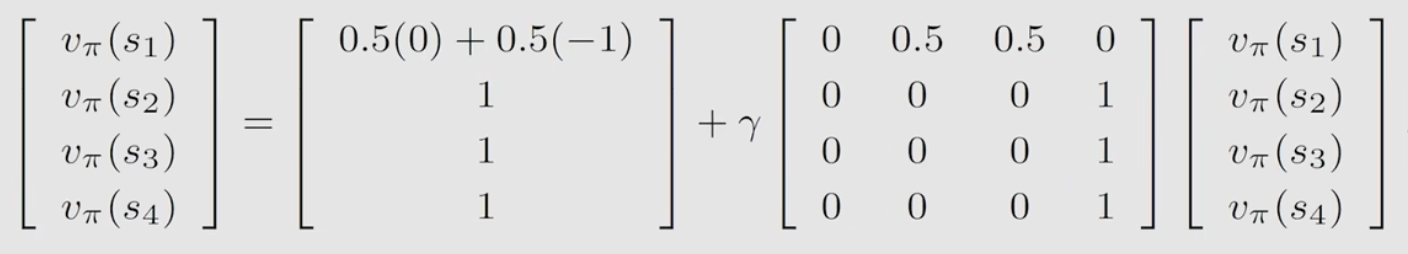
如何求解

为何要求？因为求每个状态的state value是为了评价一个策略的好坏的。只有能够评价一个策略的好坏，才能够找到最优策略，因此状态值其实是强化学习的一个基本问题，而贝尔曼公式即是解决方法之一

直接法

对于矩阵形式

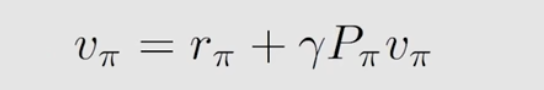
可以通过矩阵求解法，直接获得

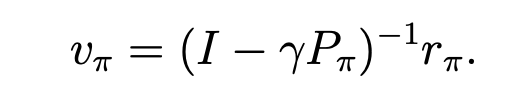
迭代法

当矩阵大的时候，求逆操作代价大，因此迭代法更加通用。

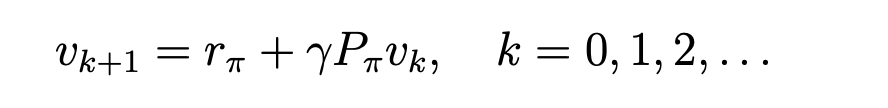
如上式，在初始时刻，对每一个状态的state value随机赋一个初始值。

然后将初始值代入右侧，便可得到左侧的下一次迭代的新state value。

再将新获得的state value 代入右侧，如此往复，最可获得近似最终的状态值。

迭代法为何可求得最终的state value呢？proof 过程请付费收听。