1.1 State Values and Bellman Equation (Basic and Definition)

前置知识

从某一个状态出发，获得的return的和即为该状态的状态值v

Return

• 什么是return：沿某一个路径走，所有的discounted reward之和,比如下面这个图，如果不加discount，那第一个图中，从s1出发，return就是2。

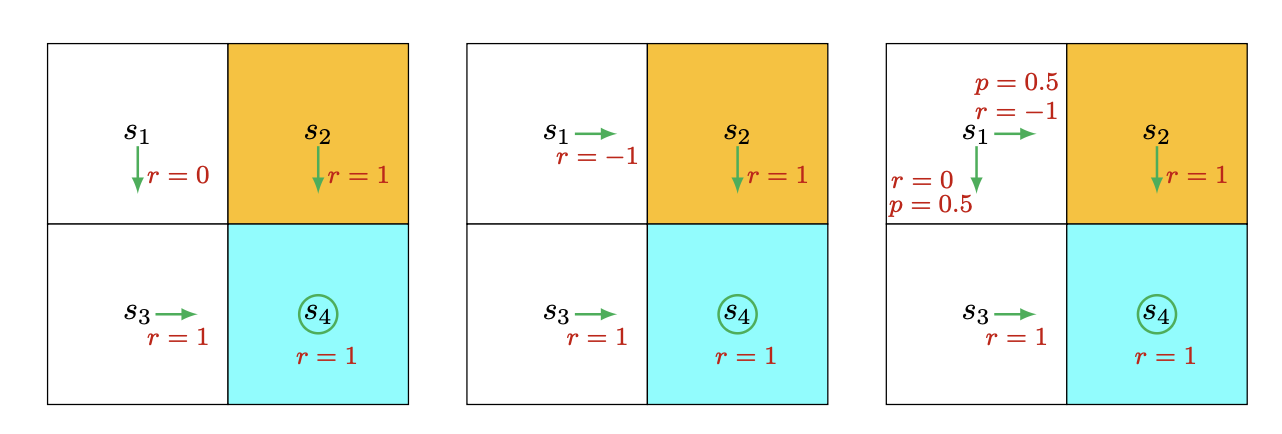
• 为什么return 重要？ 上面3个策略中，直观上如果从s1出发，可以看到每一个图策略最好，第二个最差（会进入到黄色的forbiden area），return是用来帮助我们从数学上评估策略的好坏。

s4是终点，如果会在s4处一直循环，则这3个图的return分别为：

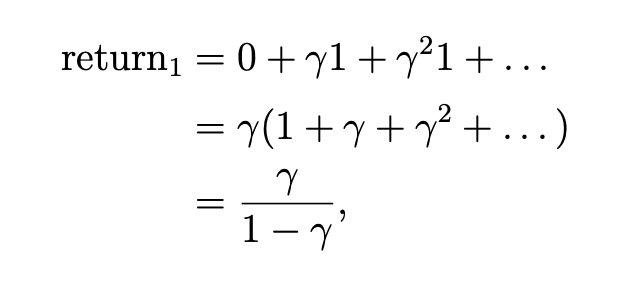
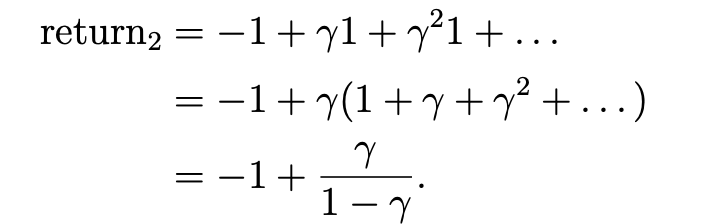
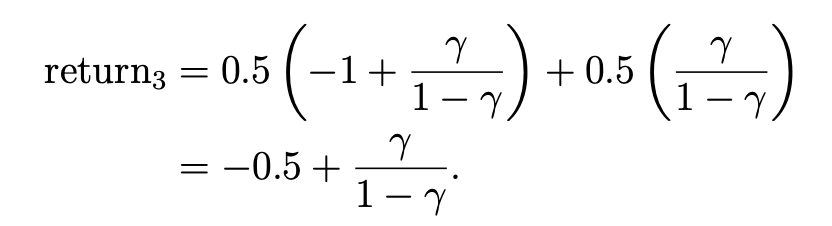
可以看到第一个大于第三个大于第二个

如何计算return

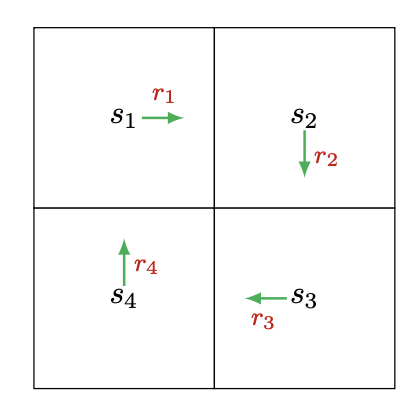
针对这个策略，如何计算由每个状态开始的return?

直接法

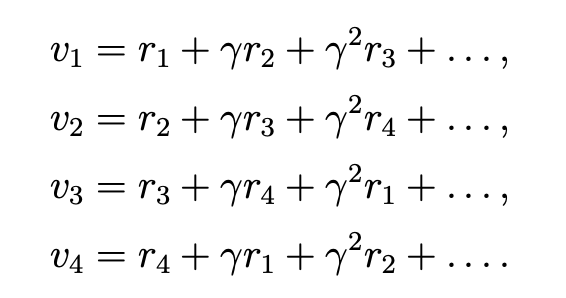
迭代法

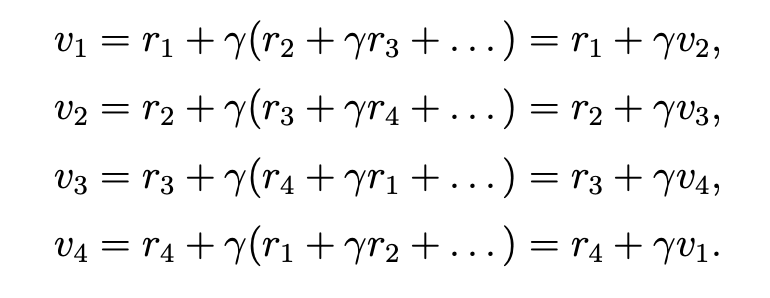
这种迭代法的公式是我们想要的，因为其可以通过bootstrapping方法求得最优策略

bootstraping

迭代法的式子可通过矩阵描述为：

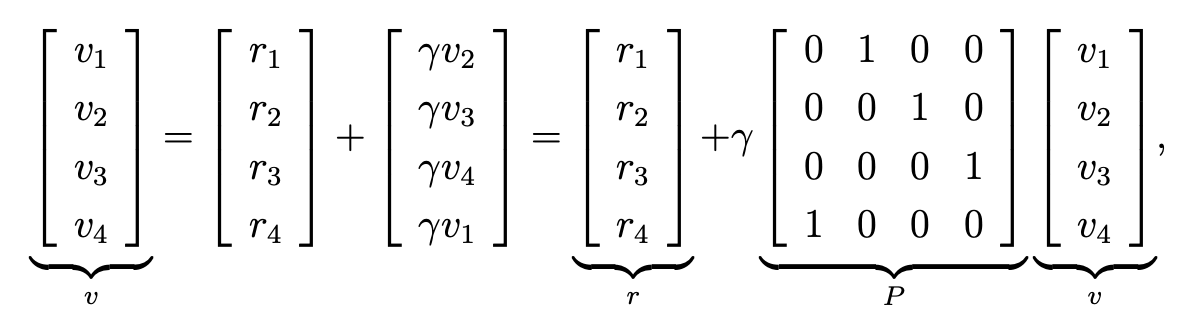
最终获得的简洁式子为：

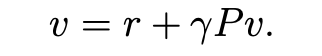
在这个式子里，r是给定的，\(\gamma\) 也是给定的，\(v\)是我们要求的，可以通过一个初始值给定，P 可以根据策略生成

状态值是什么

单步概念

了解这个单步中，每个字母及下标的意思

多步概念

对于一个多步的trajectory, 它的每一步的discounted reward之和，即是return, 使用\(G_t\)表示

state value

即为\(G_t\)的期望，表示如下：

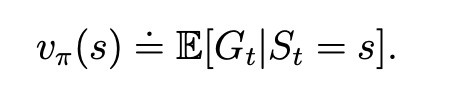
• return和state value区别：return是单个trajectory，state value为多个trajectory的return再求平均值。如果从某个状态出发，只会有一个trajectory，那return 和 state value其实是一样的

见下面的例子

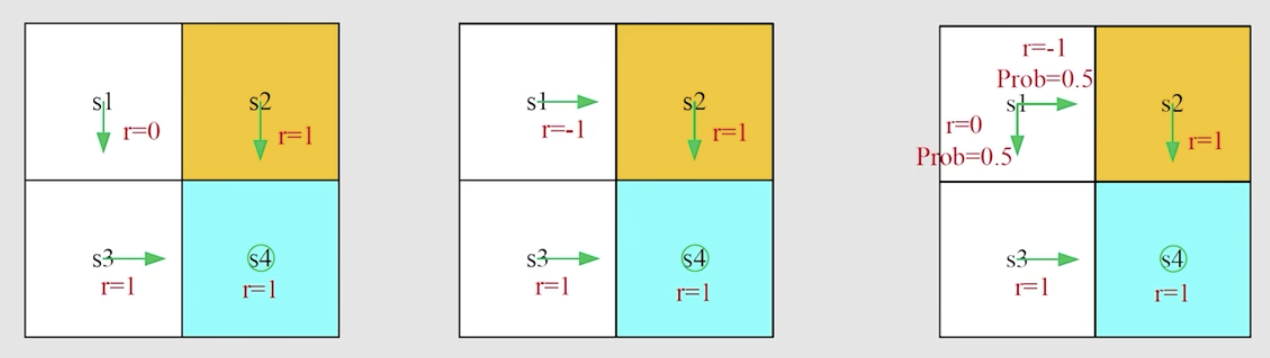
这三个策略的状态值计算如下：

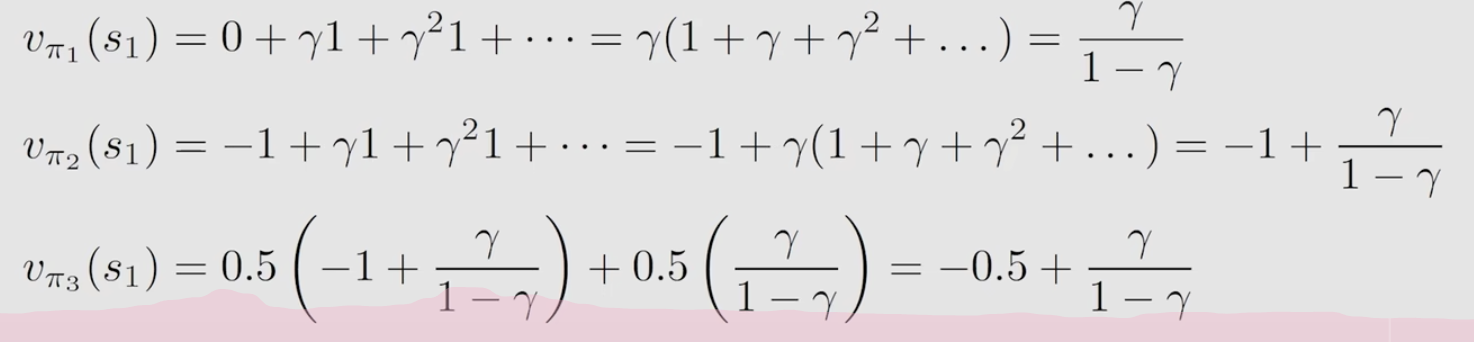
第一个和第二个的return和state value其实是一样的。在第3个策略中，由于在s1的下一步处有一个分裂，因此这个策略的state value即为分裂出来不同支的return的期望，即按概率乘上每一个trajectory的return。

贝尔曼公式, Bellman Equation

描述不同状态的state value之间的关系。

对于一个状态\(S_t\)，它的trajectory为：

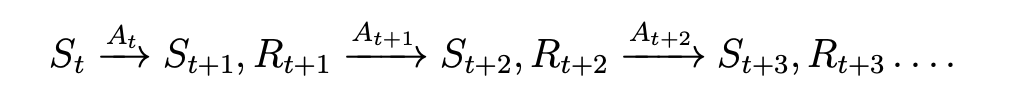
则它的return可以描述为：

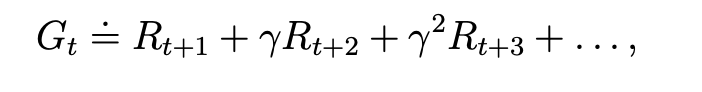
将这个return描述成迭代式：

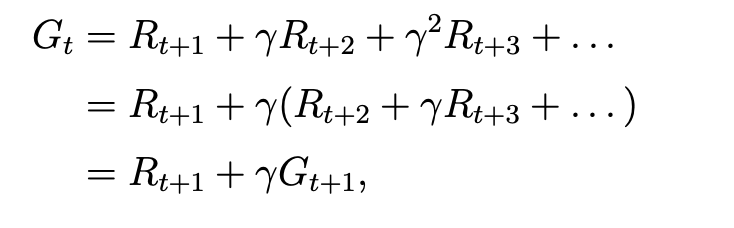
state value 的计算为它的期望，表示为：

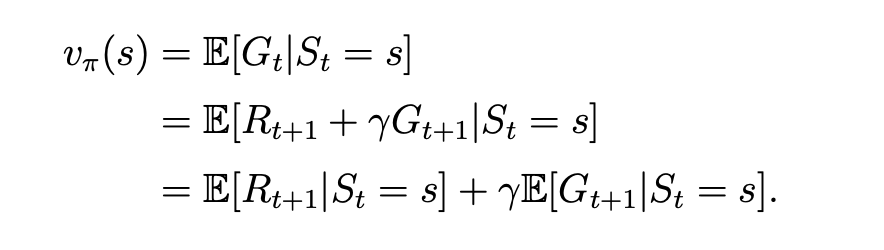
2项分开来看

• 第一项

每一项即为当下状态到下一个状态，所有可能的reward的mean，即为：

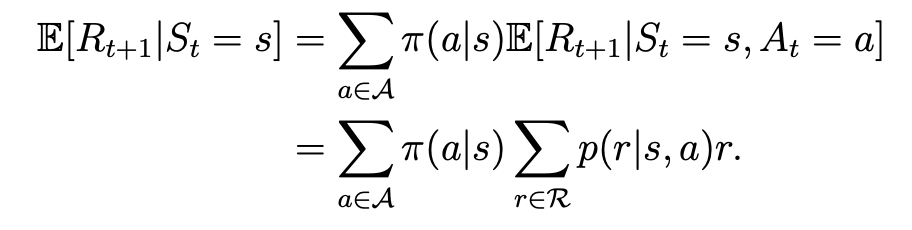
在状态s，可能会有多个action，每个action概率 \(\pi (a|s)\), 而采取每个action又会获得一个reward，获取reward 为 r 的概率：\(p(r|s,a)\).

• 第二项

第二项为future rewards的mean,表示为：

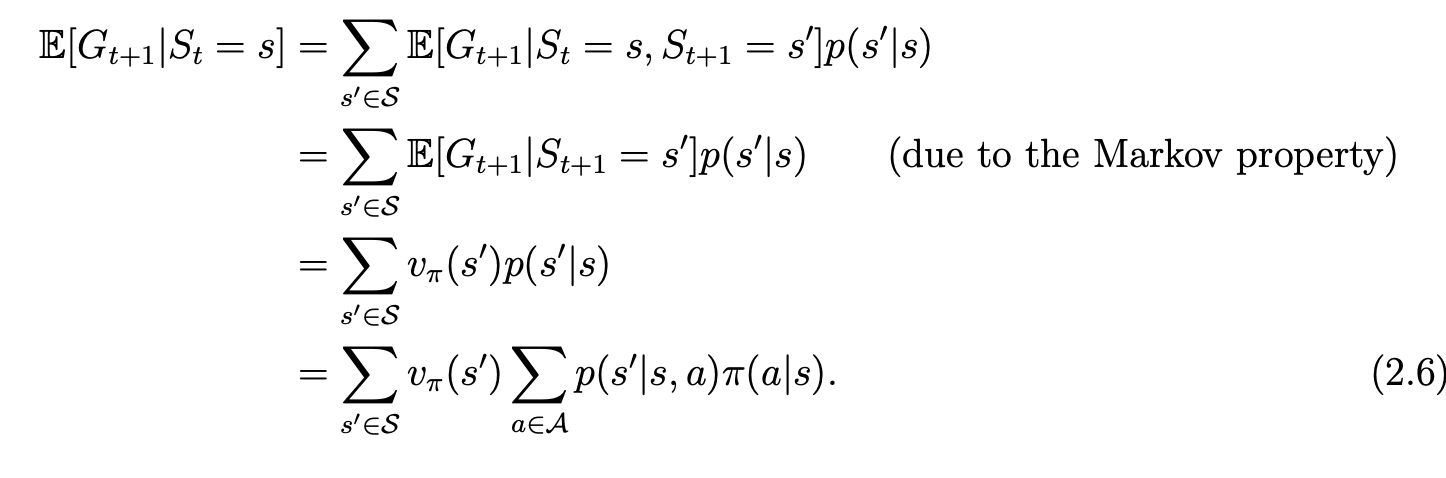
这个式子意思为：在当下状态采取动作a（有个概率），会跳到下一个状态s’（有个概率）,再计算在s’状态时的state value，再对前面所有的结果取一个mean（即所有可能的下一个状态都要算上，因此有一个求和符号）

因此合在一起的最终结果：

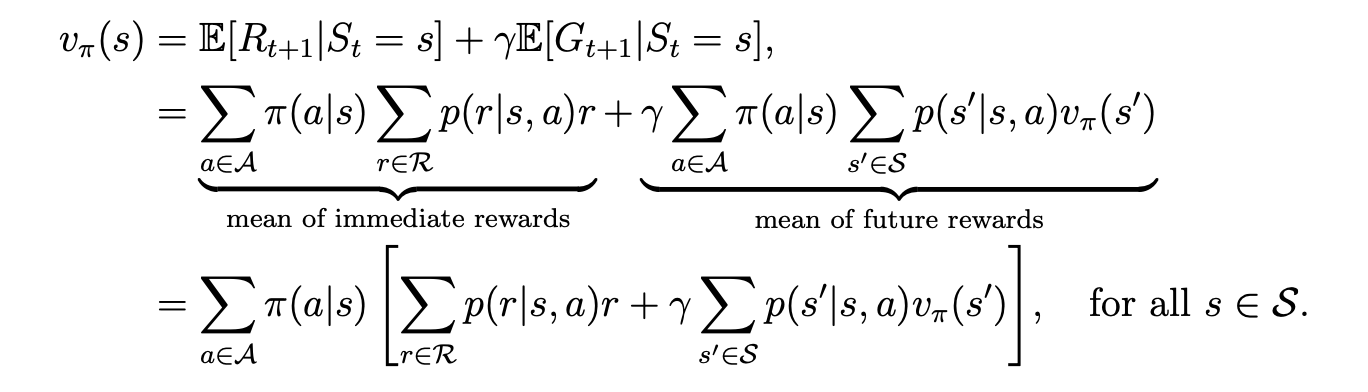
这个式子是对每一个状态都适用的，通过将每个状态的结果联立，最后可获得每一个状态的state value.

以前只觉得公式这个东西，只是对一个理论的简单记法，其实不然。如果逻辑正确，通过一套正确的公式推理，是可以推导出新的理论的，就像麦克斯伟的电磁理论，完全基于公式推理